本帖最後由 跑跑小流星 於 2015-2-26 23:36 編輯
令線段AE, 線段BF之交點為G, 線段BD, 線段CE之交點為H
因為線段BF // 線段CE, 故角ABG=角BCH; 因為線段AE // 線段BD, 故角BAG=角CBH 三角形內角和為180度, 故角AGB=角BHC 所以三角形ABG及三角形BCH為相似三角形. 故 線段AG/線段BH =線段BG/線段CH… (1)
因為 線段BF // 線段CE, 故角GFE=角HED 因為 線段AE // 線段BD, 故角GEF=角HDE 三角形內角和為180度, 故角FGE=角EHD 所以三角形FGE及三角形EHD為相似三角形. 故 線段GF/線段HE = 線段GE/線段HD … (2)
因為 線段BF // 線段CE, 線段AE // 線段BD, 故BHEG為平行四邊形 所以角BGE=角BHE, 即角AGF=角CHD …(3) 補充:
因為角BGE+角AGB=180度, 且角AGB+角AGF=180度
故角BGE+角AGB=角AGB+角AGF => 角BGE=角AGF
因為角BHE+角BHC=180度, 且角BHC+角CHD=180度
故角BHE+角BHC=角BHC+角CHD => 角BHE=角CHD
故角AGF=角CHD
且 線段BG=線段HE, 線段BH=線段GE
故(1)式可改寫為 線段AG/線段GE = 線段HE/線段CH => 線段AG*線段CH=線段HE*線段GE… (4)
(2)式可改寫為線段GF*線段HD=線段GE*線段HE… (5)
由(4), (5)可知 線段AG*線段CH=線段GE*線段HE=線段GF*線段HD => 線段AG*線段CH=線段GF*線段HD
=> 線段CH=(線段GF*線段HD)/線段AG (等號兩邊同除線段AG, 線段AG長不為0, 故可除)
=> 線段HD/線段AG=線段CH/線段GF …(6) (等號兩邊同除線段GF, 線段GF長不為0, 故可除)
由(3)式及(6)式可知, (式3證明角度AGF=DHC相等, 式6證明兩組邊成比例)
三角形AGF及三角形DHC為相似三角形 (SAS)
故角AFG=角HCD … (7) 角FAG=角HDC … (8)
綜合以上結果: 角AFE+角CDE =角AFG+角GFE+角EDH+角HDC (將角分解) =角AFG+角GFE+角GEF+角FAG (代入8式) =角FAG+(角AFG+角GFE)+角GEF (整理) =180度 (三角形AFE內角和)
即角AFE與角CDE互補, 故 線段AF//線段CD
| 
 飄移 3/27 更新總覽(4/3 更新)
飄移 3/27 更新總覽(4/3 更新)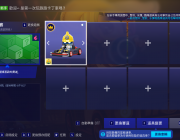 3/13 維護提醒 + 更新說明
3/13 維護提醒 + 更新說明 飄移 3/20 更新總覽
飄移 3/20 更新總覽 3/20 維護提醒 + 更新說明
3/20 維護提醒 + 更新說明 3/20 更新:時間商店限時開放 馬拉松 迅 疾速登場
3/20 更新:時間商店限時開放 馬拉松 迅 疾速登場 3/13 遊戲內活動 + DAY ONE聯賽 + 商店更新
3/13 遊戲內活動 + DAY ONE聯賽 + 商店更新

 提升卡
提升卡 變色卡
變色卡 千斤頂
千斤頂
 每次都考60分已 下...
每次都考60分已 下...